Is it possible to control market risk

Derivative market extends. There is a difficulty to grasp the risk level of a new commercial bond in complete produced by derivative market. There might be a case the market has insufficient liquidity to approve a leverage of the derivatives.

VaR is defined as expected loss in response to market changes at a certain period in case that the portfolio does not change in the period.

ΔhPtof above equation shows expected P/L(Profit and Loss) for next n-days.

although it is impossible to see exact behavior how risk factor of underlying asset changes for further n-days from now, we can assume some situation. We expect Historical volatility and its correlation continue changes. The possiblity of risk factor changes collects a distribution ΔhPt as a set of variables of P/L in portfolio pricing model.

VaR level is a stochastic value of VaR measurement that corresponds to a expected frequency of given level of loss happened.

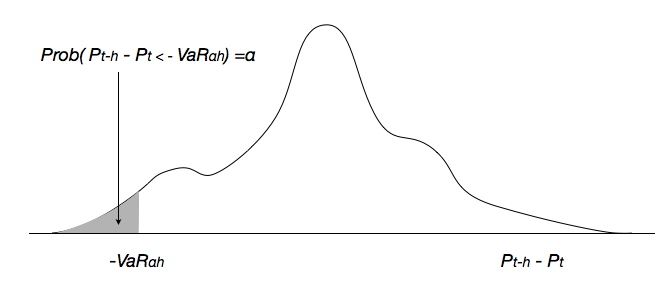
VaR is measured down side percentage of a theoretical P/L distribution that will be happened by risk factor changes in the market. The loss of portfolio is left side of the n-days risk axis.

100α％ h-days VaR is x of next equation;

An oblique line area α of next fugure, the cut off point is -VaR α h

CONT.